70以上 a^3+b^3+c^3-3abc formula proof 261432-A^3+b^3+c^3-3abc formula proof

Show activity on this post We have a3 b3 c3 − 3abc = det (a b c c a b b c a) = (a b c)(a ωb ω2c)(a ω2b ωc) where ω = exp2πi 3 is a primitive third root of unity On the other hand a b c = ex, a ωb ω2c = eωx, a ω2b ωc = eω2x and 1 ω ω2 = 0, hence a3 b3 c3 − 3abc = e0x = 1Adding like terms, the final formula (worth remembering) is (a b c) 2 = a 2 b 2 c 2 2ab 2bc 2ac Practice Exercise for Algebra Module on Expansion of (a b c) 2What is formula of a3b3 Math Algebraic Expressions and Identities NCERT Solutions;

A 3 B 3 C 3 3abc Formula

A^3+b^3+c^3-3abc formula proof

A^3+b^3+c^3-3abc formula proof-The square of the sum of three or more terms can be determined by the formula of the determination of the square of sum of two terms Now we will learn to expand the square of a trinomial (a b c) Let (b c) = x Then (a b c) 2 = (a x) 2 = a 2 2ax x 2So, a3 b3 c3 3abc = 0 (a b c ) (a2 b2 c2 ab ac bc) = 0 this means either (a2 b2 c2 ab ac bc) = 0 or (a b c ) = 0 (a2 b2 c2 ab ac bc) = 0 cannot be zero because 2a² 2b² 2c² 2ab 2ac 2bc = 0 a² b² 2ab a² b² 2c² 2ac 2bc = 0

Http Www Stevens Edu Ssm Dec4 Pdf

Fermat's Last Theorem is a theorem in number theory, originally stated by Pierre de Fermat in 1637 and proved by Andrew Wiles in 1995 The statement of the theorem involves an integer exponent n larger than 2 In the centuries following the initial statement of the result and before its general proof, various proofs were devised for particular values of the exponent n= a 3 b 3 3ab(a b) On solving it further we get a 3 b 3 3a 2 b 3ab 2 Hence, in this way we obtain the identity ie (a b) 3 = a 3 b 3 3ab(a b) = a 3 b 3 3a 2 b 3ab 2 Example 1 Solve (3a 2b) 3 Solution This proceeds as Given polynomial (3a 2b) 3 represents the identity (a b) 3 Where a = 3a and b = 2b NowThe left hand side proof is tricky but here it is, although it would be much easier to use the right hand side given a^3 b^3 c^3 3abc factor a^3 b^3 using cubic formula (ab) (a^2 ab

A 3 b 3 c 3 3abc = (a b c)(a 2 b 2 c 2 ab bc ca) Where a = 2a, b = 3b and c = 5c Now apply values of a, b and c on the LHS of identity ie a 3 b 3 c 3 3abc = (a b c)(a 2 b 2 c 2 ab bc ca) and we get = (2a 3b 5c) { (2a) 2 (3b) 2 (5c) 2 (2a)(3b) (3b)(5c) (5c)(2a) } Expand the exponential forms and we getA 3 b 3 c 33abc=(ab) 33a 2 b3ab 2 c 33abc =(abc) 3 3(ab) 2 c3(ab)c 2 3ab(abc) =(abc) 3 3(ab)c(abc)3ab(abc)=(abc)(a 2 b 2 c 2 abbcac)Scalar or pseudoscalar Although the scalar triple product gives the volume of the parallelepiped, it is the signed volume, the sign depending on the orientation of the frame or the

Since the LHS is symmetric in a, b, c, and the RHS can be written as ( ( a b c) − 3 a 2) 3 it suffices to prove the inequality with the additional assumption a ≤ b ≤ c Replacing a, b, c by a, a x, a x y, respectively (where x, y ≥ 0 ), we getSo basically what it is is that the problem is a^3b^3=c^3 but you changed it to cube root a^3 cube rootb^3 =cube rootc^3 which is equal to ab=c, so if what you say is right you would be able to use any terms for this second equation and it would fit the third so lets say 11=2 then plug in you get 11=8 doesn't work753 x 753 x 753 247 x 247 x 247

If A 1 3 B 1 3 C 1 3 0 Then A A B C 0 B A B C 3 27 A B C C A B C 3 Youtube

What Are Various Forms To Write A B C A Whole Cube Quora

A 3 b 3 c 3 − 3abc = (a b c) (a 2 b 2 c 2 − ab − bc − ac) If (a b c) = 0, a 3 b 3 c 3 = 3abc2 29 if a ib=0 wherei= p −1, then a= b=0 30 if a ib= x iy,wherei= p −1, then a= xand b= y 31 The roots of the quadratic equationax2bxc=0;a6= 0 are −b p b2 −4ac 2a The solution set of the equation is (−b p 2a −b− p 2a where = discriminant = b2 −4ac 32A^3 b^3 c^3 3abc = (a b c) (a^2 b^2 c^2 ab ac bc) By assumption a^3b^3c^3=3abc so the left hand side is 0 Therefore (abc) (a^2b^2c^2abacbc) = 0 So either abc=0 or

Algebra Formulas A B 3 A B 2 A B C 3 A 3 B 3 Teachoo

Prove That A3 C3 3abc A B C B2 C2 Ab Ac By Taking Lhs Brainly In

Example 22 If a b c = 0, then prove that a 3 b 3 c 3 = 3abc Solution We know that Example 23 Find the following product (x y 2z) (x 2 y 2 4z 2 – xy – 2yz – 2zx) Solution We have, Example 24 If a b c = 6 and ab bc ca = 11, find the value of a 3 b 3 c 3 – 3abc SolutionIf A is an elementary matrix and B is an arbitrary matrix of the same size then det(AB)=det(A)det(B) Indeed, consider three cases Case 1 A is obtained from I by adding a row multiplied by a number to another row In this case by the first theorem about elementary matrices the matrix AB is obtained from B by adding one row multiplied by a number to another rowFurther more, note that the yellow part is a cuboid with height a, width a, and length b ;

What Is The Formula Of Math A 3 B 3 Math Quora

What Is The Formula Of Math A 3 B 3 Math Quora

Thx Socratic Prove that a3 b3 c3 − 3abc = (a b c)(a2 b2 c2 − ab − bc − ca)This restates in vector notation that the product of the determinants of two 3×3 matrices equals the determinant of their matrix product As a special case, the square of a triple product is a Gram determinant;A 3 ± b 3 = (a Same sign b)(a 2 Opposite sign ab Always Positive b 2) Note The quadratic portion of each cube formula does not factor, so don't waste time attempting to factor it Yes, a 2 – 2ab b 2 and a 2 2ab b 2 factor, but that's because of the 2 's on their middle terms

If A B C 5 And Ab Ca 10 Then Prove That A 3 B 3 C 3 3abc 25 Youtube

Inequalities Marathon

Ashutosh Verma, Meritnation Expert added an answer, on 24/7/14 Ashutosh Verma answered this Answer Factorise a 3 b 3 c 3 3abc We know ( a 3 b 3 ) = ( a b ) ( a 2 ab b 2 ) So we rearrange it As ⇒ ( a b ) ( a 2 ab b 2 ) c 3 3abc ⇒ ( a b ) ( a 2 2 ab b 2 3ab) c 3 3abcUsing the formula, a^3 b^3 c^3 = (a b c) (a^2 b^2 c^2 ab bc ca) 3abcIf abc=0,then a^3 b^3 c^3 = 3abcabca3b3c3 = 3abca3 abcb3 abcc3 = 3bca2 cab2 abc2 = 3Answer (C) 3 Answer verified by Toppr Upvote (70)Thx Socratic Prove that a3 b3 c3 − 3abc = (a b c)(a2 b2 c2 − ab − bc − ca)

Factorization Of The Form A3 C3 3abc Youtube

Inequalities Marathon

1 Vipan Sharma, added an answer, on 6/11/17 Vipan Sharma answered this Please note that a3=a 3 , b3=b 3 and c3=c 3 Solution Let f (a)= a3b3c3−3abc be a function in a Now, putting a = (bc), we get f ( (bc)) = b3c3 (bc)3 3bc (bc) = (bc)3 (bc)3 = 0 Hence, by factor theorem, (abc) is a factorSolution 297 x 297 = (300 – 3) (300 – 3) = (300 – 3) 2 = 300 2 3 2 – 2x3x300 = 297 x 297 = 9 – 1800 = 809 Question 753 x 753 247 x 247 753 x 247 = ?We are going to share the \( a^3 b^3 \) algebra formulas for you as well as how to create \( a^3 b^3 \) and proof we know that what is the formulas of \((ab)^3 \) use the of this formula to prove a cube plus b cube formula

If A B C 0 Then A 3 B 3 C 3 0 How Quora

Verify A3 C3 3abc 1 2 A B C A B 2 B C 2 C A 2 Brainly In

In this section, you will learn the formula or expansion for (a 3 b 3)We already know the formula/expansion for (a b) 3 That is, (a b) 3 = a 3 b 3 3ab(a b) Case 1 (a b) 3 = a 3 b 3 3ab(a b) Subtract 3ab(a b) from each sideClass 9 Maths Prove a^3 b^3 c^3 3abc = (a b c) (a^2 b^2 c^2 ab bc ca) rb classes YouTubeNote that in the above diagram, the red part itself is a cube with volume a 3 and the blue part is a cube with volume b 3;

What Is The Expansion Of A B C 3 Quora

The Value Of A Cube Plus B Cube Plus C Cube Minus 3 Abc If A B C Is Equals To 15 And A B Ca Brainly In

Prove that a^3b^3c^33abc= (abc) (a^2b^2c^2abbcca) How can I solve this without expanding everything?A^3 b^3 c^3 3abc = (abc) (a^2 b^2 c^2 ab bc ac) = (abc) { (a^2b^2c^2 2ab2bc2ac) 3 (abbcac) } = (abc) { (abc)^2 3 (abbcac) } = (abc)^2 3 (abbcac) (abc) = (abc)^2 3a^2b 3ab^2 3abc 3abc 3b^2c 3bc^2 3a^2c 3abc 3ac^25 (a 3 b 3) = (a b)(a 2 ab b 2) 6 (a 3 b 3) = (a b)(a 2 ab b 2) 7 (a 3 b 3 c 3 3abc) = (a b c)(a 2 b 2 c 2 ab bc – ac) Question 297 x 297 =?

Q Tbn And9gcqjzcetssknl5tvsoa3aopkacdjcpfoq4fwy2ldp Eugpth9 Fq Usqp Cau

2 Two Cube 5 Five Cube 10 Ten Cube Pdf Free Download

Thus the cuboid has volume a x a x b = a²b, and as the diagram has 3 yellow cuboids, the total volume of the yellow part would be 3a²bSince the LHS is symmetric in a, b, c, and the RHS can be written as ( ( a b c) − 3 a 2) 3 it suffices to prove the inequality with the additional assumption a ≤ b ≤ c Replacing a, b, c by a, a x, a x y, respectively (where x, y ≥ 0 ), we getPerhaps you were confused or misled by the word "derive" here Sometimes, when asked to derive or prove an equation, all that is being asked for is that you check that the two sides of the equation are indeed equal by 'multiplying out' any complex terms (the right hand side in this case) and ending up with the same term on each side So @JasperLoy's simple answer would (by my lights) do just fine

A B C Is Equal To 9 And A Square B Square C Square Is Equal To 35 Find The Value Of A Cube Brainly In

Ab Ca Does Not Exceed Cc

= (a b)(a b)(a b) = (a b)(a² ab ab b²) = (a b)(a² 2ab b²) = a³ 2a²b ab² a²b 2ab² b³ = a³ 3a²b 3ab² b³A 3 b 3 c 3 We can choose three "a"'s for the cube in one way C(3,3)=1, or we can choose an a from the first factor and one from the second and one from the third, being the only way to make a3 The coefficient of the cubes is therefore 1 (It's the same for a, b and c, of course) 3a 2 b3a 2 c Next, we consider the a 2 terms We can chooseProve that a^3b^3c^33abc= (abc) (a^2b^2c^2abbcca) How can I solve this without expanding everything?

Inequalities Marathon

If The Roots Of The Equation C 2 Ab X 2 2 A 2 X B 2 Ac 0 Are Equal Prove That Either A 0 Or A 3 B 3 C 3 3abc Sarthaks Econnect Largest Online Education Community

A 3 B 3 C 3 3abc Formula Proof Using Properties Of Determinants Prove That A B C A B B C C A A 3 B 3 C 3 3abc B C C A A B Mathematics Topperlearning Com Dteg67ff If A B C 6 And Ab Ca 11 Is Given Then Find The Value Of A 3 B 3 C 3 3abc YoutubeFactoring a 3 b 3 An expression of the form a 3 b 3 is called a difference of cubes The factored form of a 3 b 3 is (a b)(a 2 ab b 2) (a b)(a 2 ab b 2) = a 3 a 2 b a 2 b ab 2 ab 2 b 3 = a 3 b 3 For example, the factored form of 27x 3 8 (a = 3x, b = 2) is (3x 2)(9x 2 6x 4) Similarly, the factored form of 125x 327y 3 (a = 5x, b = 3y) is (5x 3y)(25x 2 15xy 9y 2)3(a b)3 = a3 b3 3ab(a b) 4 (a b) 3 = a3 b3 3ab(a b) 5(a b c)2 = a2 b2 c2 2ab2bc 2ca 6(a b c)3 = a3 b3 c33a2b3a2c 3b2c 3b2a 3c2a 3c2a6abc 7a2 b2 = (a b)(a – b ) 8a3 – b3 = (a – b) (a 2 ab b2 ) 9a3 b3 = (a b) (a 2 ab b2 ) 10(a b)2 (a b) 2 = 4ab 11(a b)2 (a b) 2 = 2(a 2 b2 )

Inequalities Anthony Erb By Arturo Portnoy Issuu

Inequalities Marathon

//enwikipediaorg/wiki/Complex_number https//enwikipediaorg/wiki/Root_of_unity For this case, the complex number z such that z^3 = 1 ie, z = exp (i*pi*2/3) Then a^3 b^3 c^3 3abc = (a b c) (a z b z^2 c) (a z^2 b z c) Show more AnonymousFermat's Last Theorem is a theorem in number theory, originally stated by Pierre de Fermat in 1637 and proved by Andrew Wiles in 1995 The statement of the theorem involves an integer exponent n larger than 2 In the centuries following the initial statement of the result and before its general proof, various proofs were devised for particular values of the exponent nThe Cardano's formula (named after Girolamo Cardano ), which is similar to the perfectsquare method to quadratic equations, is a standard way to find a real root of a cubic equation like a x 3 b x 2 c x d = 0 ax^3bx^2cxd=0 a x 3 b x 2 c x d = 0 We can then find the other two roots (real or complex) by polynomial division and the quadratic formula The solution has

If A B C 0 Then A 3 B 3 C 3 0 How Quora

If A B C 0 Then A 3 B 3 C 3 0 How Quora

3 = a 3 b 3 3ab(a b) a 3 b 3 c 3 3abc = (a b c)(a 2 b 2 c 2 ab bc ca) Before you understand (a b c) 2 = a 2 b 2 c 2 2ab 2bc 2ca, you are advised to readProof Of The Formula For A 3 B 3 Save Image Algebra Formulas A B 3 A B 2 A B C 3 A 3 B 3 Teachoo Save Image What Is The Formula Of Math A 3 B 3 Math Quora Save Image Proof Of A B 3 A3 3a2b 3ab2 Proof Of A B 3 Formula Youtube Save Image Pin On Cube Save ImageWe are given that a^3 b^3 c^3 = 3*abc, where a,b,c are positive Now a^3 b^3 c^3 3abc = (a b c)* (a^2 b^2 c^2 ab ac bc) But a^3 b^3 c^3 3abc = 0, and since (a b c)

2 Two Cube 5 Five Cube 10 Ten Cube Pdf Free Download

If A B C 0 Then Prove That A3 C3 3abc Youtube

(a b c) 3 = a 3 b 3 c 3 3(a b)(b c)(c a) a 3 b 3 c 3 − 3abc = (a b c) (a 2 b 2 c 2 − ab − bc − ac) Power n Formula(xiii) a 3 b 3 c 3 – 3abc = (a b c)(a 2 b 2 c 2 – ab – bc – ca) CBSE Class 10 Maths Important Questions with Solutions for Board Exam 21 3Example Solve 8a 3 27b 3 125c 3 – 90abc Solution This proceeds as Given polynomial (8a 3 27b 3 125c 3 – 90abc) can be written as (2a) 3 (3b) 3 (5c) 3 – 3(2a)(3b)(5c) And this represents identity a 3 b 3 c 3 3abc = (a b c)(a 2 b 2 c 2 ab bc ca) Where a = 2a, b = 3b and c = 5c Now apply values of a, b and c on the LHS of identity ie a 3 b 3 c 3

Find The Value Of A3 C3 3abc If A B C 15 And Ab Ca 74 Brainly In

Proof The Algebraic Formula A3 C3 3abc A B C B2 C2 Ab Ca Youtube

An algebraic identity is an equality that holds for any values of its variables For example, the identityLogin Create Account Class8 » Math Algebraic Expressions and Identities what is formula of a 3 b 3 Share with your friends Share 1381 a 3 b 3 =(ab)(a 2 b 2ab) 14 ;Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history

Www Maa Org Sites Default Files Pdf Putnam 19 Putsol19a Pdf

Proof Of A3 C3 3abc When A B C 0 Youtube

I meant prove a^3b^3c^3>=3abc using w=(xyz)^(1/3) and yes i did mean earlier >=

A 3 B 3 C 3 3abc Formula

Class 9 Maths Prove A 3 B 3 C 3 3abc A B C A 2 B 2 C 2 Ab Ca Rb Classes Youtube

Class 9

If A B C 0 Then How Can You Prove A 3 B 3 C 3 3abc Quora

Prove That A3 C3 3abc A B C B2 C2 Ab Ca 1 2 A B C A B 2 B C 2 C A 2 Youtube

A 3 B 3 C 3 3abc Formula Proof

If A B C 5 And Ab Ca 10 Prove A 3 B 3 C 3 3abc 25 Cbse Class 9 Maths Learn Cbse Forum

Mualphatheta Org Upload Files Pdf Titufall06 Pdf

最新ab Ca ただぬりえ

A 3 B 3 C 3 3abc Formula Proof

Algebraic Identities Of Polynomials A Plus Topper

Using Properties Of Determinants Prove That A B C A B B C C A A 3 B 3 C 3 3abc B C C A A B Mathematics Topperlearning Com Dteg67ff

A B C 3 Proof

Let Q A3 C3 3abc Where A B And C Are Positive Integers If N Is The Minimum Positive Value Of Q Then What Is N Greater Than Quora

A B C 3 Formula Proof

Expansions I Love Maths

Prove That A B C 3 A 3 B 3 C 3 3 A B B C C A Youtube

A B C 3 Proof

A 3 B 3 C 3 3abc Formula Proof

A B 3 A 3 B 3

A B A Bw A Bw2 A3

A3

A 3 B 3 C 3 3abc Formula A B 2 A 2 B 2 2ab Proof Derivation Of Algebraic Identities Youtube Youtube

If A B C 0 Then How Can You Prove A 3 B 3 C 3 3abc Quora

If A B C 5 And Ab Ac 10 Then Prove That A3 C3 3abc 25 Brainly In

Http Www Stevens Edu Ssm Dec4 Pdf

Q Tbn And9gcsn3hmt8qz Utmzoqeyjo2k4rnk95kuib8fxbhmd Uvs2llqap Usqp Cau

What Are Various Forms To Write A B C A Whole Cube Quora

If A B C 5 And Ab Ca 10 Then Prove That A3 C3 3abc 25 Studyrankersonline

A3 A3 C3 A3 C3 3abc A3 Formula

A3 A3 C3 A3 C3 3abc A3 Formula

3 C B

Prove That A 3 B 3 C 3 3abc 1 2 A B C A B 2 B C 2 C A 2

Sums Of Three Cubes Wikipedia

Find The Value Of A3 C3 3abc If A B C 5 And B2 C2 29 Brainly In

Prove That A B 3 B C 3 C A 3 3 A B B C C A 2 A 3b 3c 3 3abc Brainly In

Inequalities Marathon

Inequalities Anthony Erb By Arturo Portnoy Issuu

15 Using Properties Of Determinants Prove The Following A B C

最新ab Ca ただぬりえ

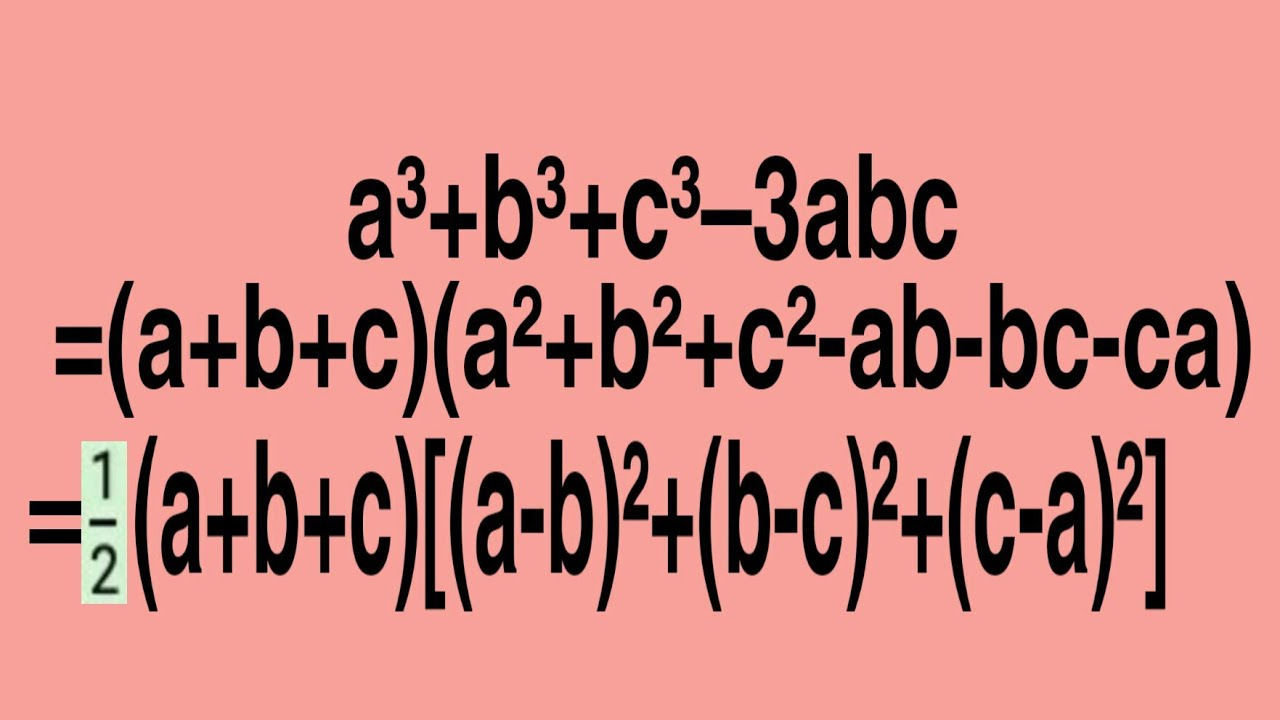
A B C 3abc A B C A B C Ab Ca 1 2 A B C A B B C C A Youtube

Inequalities Marathon

Alebra Jpg 1100 1600 Math Methods Studying Math Learning Mathematics

3 C B

This Question Is Other Than That Please Solve This Question If A1 3 B1 3 C1 3 0then Show That A B C 3 27abc Mathematics Topperlearning Com Jmf37bll

B2 C2 Formula

What Are Various Forms To Write A B C A Whole Cube Quora

If A B C 9 And B2 C2 35 Then Find A3 C3 3abc Polynomials Maths Class 9

Inequalities Marathon

Inequalities Marathon

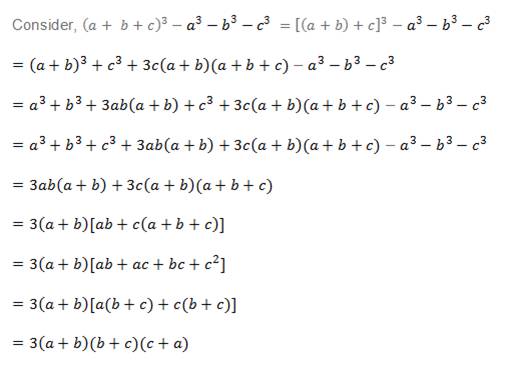
A B C 3 Proof

Special Identities A3 C3 3abc Youtube

Find The Value Of A 3 B 3 C 3 3abc If 1 A B C 8 Ab Ca 19 2 A B C 5 A 2 B 2 C 2 1 Youtube

Inequalities Marathon

A B C 3 Identity

Inequalities Marathon

2 Two Cube 5 Five Cube 10 Ten Cube Pdf Free Download

Evaluate A3 C3 3abc When A B C 6and B2 C2 24 Math Polynomials Meritnation Dubai Khalifa

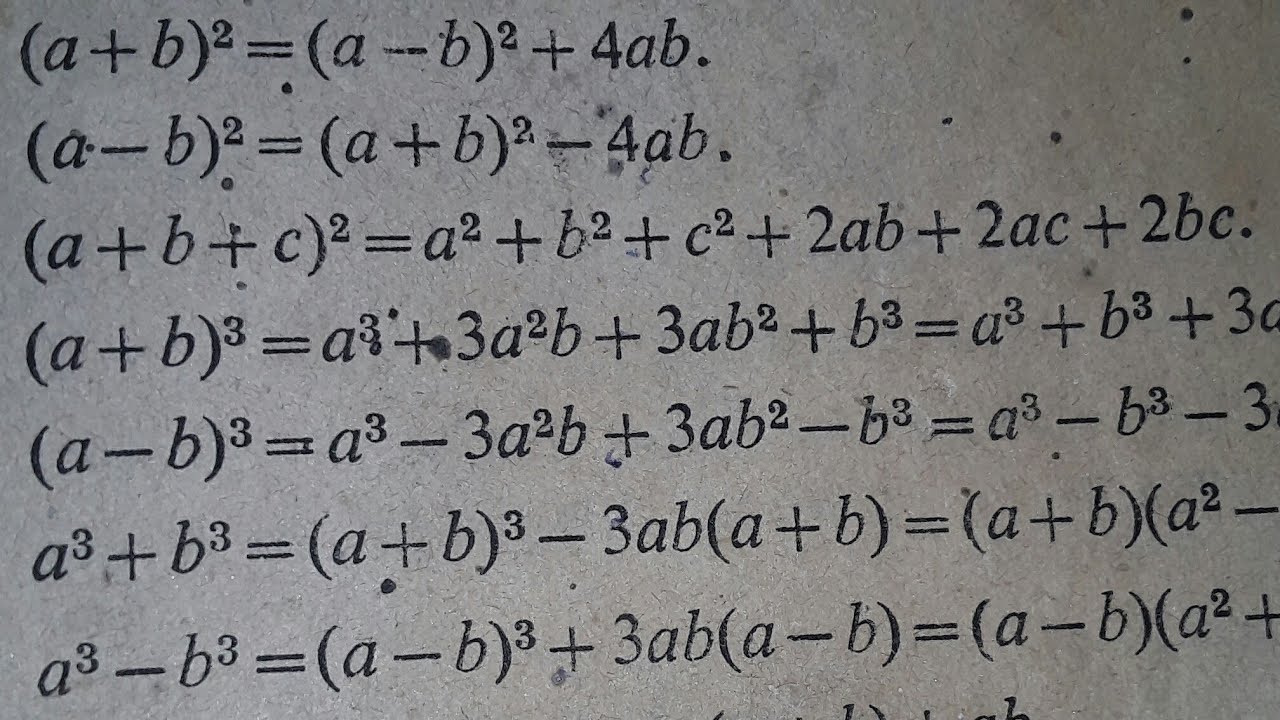
Prove That A B C 2 B2 C2 2ab

Q Tbn And9gcrwxskagpy6lndt5stu6oxp1 K0tw6brabfeaf Ncwojlvhrcb Usqp Cau

If A B C 11 And Ab Ca Then Find Se C3 3abc Brainly In

18 G11 Math E Clone Flip Book Pages 101 150 Pubhtml5

Could You Easily Decompose A 3 B 3 C 3 3abc Into The Product Of Two Polynomials With Real Coefficients

A B C 3 Proof

What Is The Expansion Of A B C 3 Quora

15 Using Properties Of Determinants Prove The Following A B C

ユニークab Ca 子供のための最高のぬりえ

A 3 B 3 C 3 3abc Formula Proof

A3 c3

Prove A3 C3 3abc A B C B2 C2 Ab Ac Youtube

A3 A3 C3 A3 C3 3abc A3 Formula

A B C 3 Formula Proof

If Math A B C 0 A 3 B 3 C 3 3 Math And Math A 5 B 5 C 5 10 Math Then Math A 4 B 4 C 4 Math Is Quora

Proof Of A3 C3 3abc When A B C 0 Youtube

Incoming Term: a^3+b^3+c^3-3abc formula proof,